A Search* – Tìm kiếm thông minh nhờ dự đoán đúng

Khi chỉ biết đi đúng chưa đủ – cần biết “đi đâu cho đáng”

Trong thế giới dữ liệu phức tạp như bản đồ, trí tuệ nhân tạo hay hệ thống robot tự hành, việc tìm đường đi nhanh nhất, ít tốn kém nhất là chưa đủ – ta cần một thuật toán có khả năng “đoán trước” con đường tốt nhất ngay từ đầu.

Đó chính là lúc A Search (A-Star Search)* phát huy sức mạnh. Đây là thuật toán tìm kiếm thông minh bậc nhất, vừa kết hợp sức mạnh của Uniform Cost Search, vừa tăng tốc bằng khả năng “tiên đoán” nhờ hàm heuristic.

A Search là gì?*

A Search* là một thuật toán tìm kiếm dựa trên chi phí tích lũy từ điểm bắt đầu kết hợp với dự đoán khoảng cách còn lại đến đích. Nó tìm ra đường đi tối ưu với tốc độ vượt trội bằng cách đánh giá tổng chi phí tại mỗi bước như sau:

f(n) = g(n) + h(n)
Trong đó:

• "g(n): chi phí thực sự từ điểm bắt đầu đến điểm hiện tại n."

• "h(n): giá trị ước lượng (heuristic) chi phí từ n đến đích (dự đoán)."

• "f(n): tổng chi phí dự kiến để đến đích thông qua n."

 

 

Ví dụ cụ thể: Tìm đường từ A đến G bằng A Search*

Bài toán:

Ta có một bản đồ gồm các thành phố kết nối với nhau, mỗi đoạn đường có chi phí (thời gian/tiền/năng lượng). Mục tiêu là tìm lộ trình rẻ nhất từ A đến G, với điều kiện dự đoán được khoảng cách từ mỗi đỉnh đến đỉnh G (tức là heuristic h(n)).

Dữ liệu đầu vào:

Đồ thị có trọng số:

Heuristic (ước lượng khoảng cách đến G):

 

Cách A hoạt động theo từng bước:*

1. Bắt đầu tại A, chi phí g(A) = 0
   → f(A) = g + h = 0 + 4.0 = 4.0

2. A có 2 lựa chọn:

   • Đi đến B: g(B) = 1.5 → f(B) = 1.5 + 3.2 = 4.7

   • Đi đến C: g(C) = 2.0 → f(C) = 2.0 + 3.0 = 5.0

   -> Chọn mở rộng B (nhỏ hơn)

3. Từ B đến D: g(D) = 1.5 (A→B) + 2 = 3.5
   → f(D) = 3.5 + 2.5 = 6.0

4. So sánh với C (f = 5.0) → mở rộng C

5. C đến D: g(D) = 2.0 (A→C) + 1 = 3.0 → f(D) = 3.0 + 2.5 = 5.5

   → D đã được mở từ B với chi phí 3.5, giờ tìm được đường rẻ hơn (3.0), cập nhật lại!

6. Từ D đến E và F:

   • E: g(E) = 3.0 + 2 = 5.0 → f(E) = 5.0 + 1.2 = 6.2

   • F: g(F) = 3.0 + 2 = 5.0 → f(F) = 5.0 + 1.8 = 6.8

7. Từ E đến G: g(G) = 5.0 + 1 = 6.0 → f(G) = 6.0 + 0 = 6.0

- Thuật toán dừng khi gặp G với f = 6.0

 

Kết quả:

• Đường đi ngắn nhất: A → C → D → E → G

• Tổng chi phí: 6.0

• A đã chọn đúng đường, không cần duyệt hết mọi khả năng như BFS hay DFS*

 

Tổng kết giá trị tại mỗi bước (minh họa dễ hiểu):

Đỉnh	g(n )	h(n)	f(n) = g(n) + h(n)
A	0	4.0	4.0
B	1.5	3.2	4.7
C	2.0	3.0	5.0
D	3.0	2.5	5.5
E	5.0	1.2	6.2
G	6.0	0	6.0

 

Tạo đồ thị minh họa A Search*

# Tạo đồ thị: G = nx.Graph()

# Thêm các đỉnh

# Thêm các cạnh và trọng số
 

# Vẽ đồ thị

Ứng dụng thực tế của A*

• Bản đồ GPS: tìm đường nhanh nhất từ vị trí A đến B.

• Trí tuệ nhân tạo (AI Game): nhân vật tìm đường di chuyển tối ưu trong bản đồ.

•  Robot & Drones: tự tìm đường di chuyển tiết kiệm năng lượng hoặc tránh chướng ngại vật.

• Giải bài toán mê cung, logic, mô phỏng...

 

Vì sao A Search “khó nhằn” với sinh viên năm nhất?*

1. Heuristic không rõ ràng:
   Nhiều bạn không hiểu h(n) lấy từ đâu, hoặc không biết làm sao để “ước lượng” cho hợp lý.

2. Nhầm lẫn với UCS hoặc BFS:
   UCS chỉ dùng g(n), BFS giả định chi phí bằng nhau → A* mạnh hơn nhờ có h(n).

3. Phức tạp khi code:
   A* cần dùng Priority Queue + quản lý đồng thời g(n), h(n) và f(n) → khiến sinh viên dễ rối logic.

4. Khó thiết kế heuristic phù hợp:
   Nếu h(n) không hợp lý (quá lạc quan hoặc bi quan) → hiệu quả giảm mạnh hoặc trả về đường sai.

 

Chiến lược học hiệu quả cho A* Search

✅ Hiểu bản chất từng thành phần f(n) = g(n) + h(n)
→ Không học thuộc – hãy tự tạo ví dụ, tự tính từng giá trị.

✅ Bắt đầu với heuristic đơn giản:
– Dùng khoảng cách Euclid (trong bản đồ), hoặc số bước còn lại trong mê cung, để quen cách xây dựng h(n).

✅ Dùng sơ đồ hoặc mô phỏng thuật toán từng bước:
→ Rất nên vẽ bảng giá trị g(n), h(n), f(n) cho từng đỉnh trong mỗi bước mở rộng.

✅ Viết lại A nhiều lần theo các tình huống khác nhau:*
– Tìm đường trong mê cung, giải sudoku, tối ưu lịch trình học,…

 

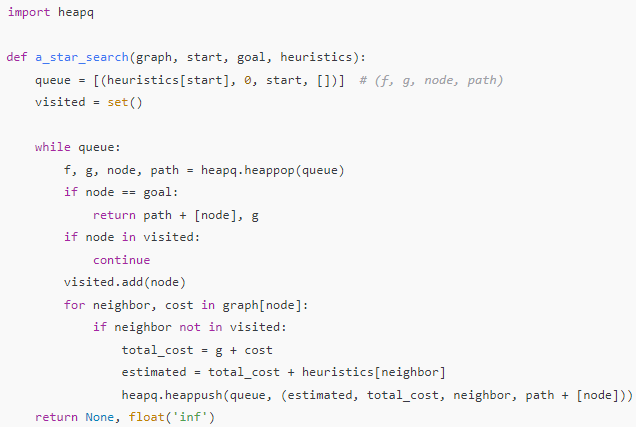
Code Python mẫu: A Search đơn giản*

 

Lời kết: Muốn tìm đường thông minh – hãy học cách “ước lượng” chính xác

A* không chỉ đơn thuần là tìm đường đi ngắn nhất – nó dạy ta kết hợp giữa dữ liệu hiện có và tư duy dự đoán tương lai. Khi bạn hiểu và sử dụng đúng thuật toán A*, bạn đang rèn luyện một trong những kỹ năng quan trọng nhất của tư duy khoa học: ra quyết định dựa trên dữ kiện và tầm nhìn chiến lược.

 

FacingX.com – Dẫn đường cho hành trình du học và học tập hiệu quả. Tại FacingX, chúng tôi không chỉ giúp bạn chuẩn bị hồ sơ du học, mà còn cung cấp các chương trình đào tạo nền tảng – giúp bạn chinh phục các môn học khó như Giải thuật, Cấu trúc dữ liệu, AI cơ bản... từ năm nhất.

---