Việc phân biệt giữa hai loại ma trận này không chỉ có ý nghĩa lý thuyết mà còn mang tính quyết định trong việc giải hệ phương trình, thiết kế thuật toán và mô phỏng trong khoa học dữ liệu.
Tuần 11: Khả nghịch – điều kiện sống còn của một ma trận / Invertierbarkeit – Wann eine Matrix „lebendig“ ist
GIỚI THIỆU | EINFÜHRUNG
VI – Tiếng Việt:
Một ma trận vuông có thể đảo ngược – hay nói cách khác là khả nghịch (invertible) – khi nó không làm mất thông tin. Ngược lại, nếu ma trận đó xẹp không gian và làm mất chiều – nó là không khả nghịch (singular). Việc phân biệt giữa hai loại ma trận này không chỉ có ý nghĩa lý thuyết mà còn mang tính quyết định trong việc giải hệ phương trình, thiết kế thuật toán và mô phỏng trong khoa học dữ liệu.
DE – Tiếng Đức:
Eine quadratische Matrix ist invertierbar, wenn sie keine Informationen verliert. Ist das nicht der Fall, nennt man sie singulär – sie „zerdrückt“ den Raum, macht ihn kleiner. Der Unterschied ist entscheidend: Invertierbarkeit bestimmt, ob Gleichungssysteme lösbar sind, ob Algorithmen stabil funktionieren oder ob eine Transformation umkehrbar ist.

KHÁI NIỆM CƠ BẢN | GRUNDLAGEN
1. Ma trận khả nghịch | Invertierbare Matrix
VI – Tiếng Việt:

DE – Tiếng Đức:

2. Ma trận không khả nghịch | Singuläre Matrix
VI – Tiếng Việt:

DE – Tiếng Đức:

CÁCH XÁC ĐỊNH & NHẬN BIẾT | WIE MAN SIE ERKENNT
VI – Tiếng Việt:
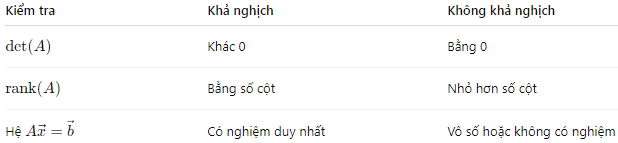
DE – Tiếng Đức:
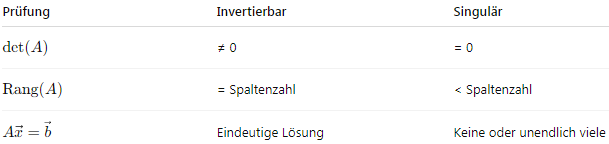
VÍ DỤ CỤ THỂ | BEISPIELE
VI – Tiếng Việt:
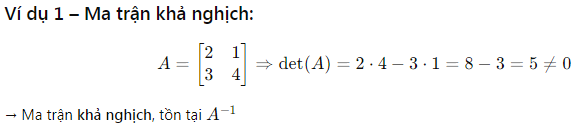
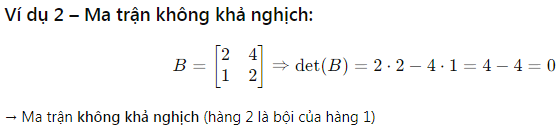
DE – Tiếng Đức:
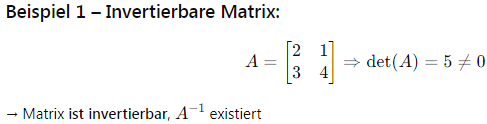
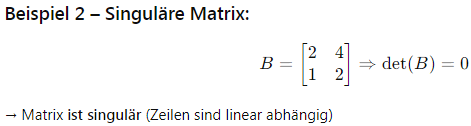
LƯU Ý CHO GIẢNG VIÊN & SINH VIÊN | HINWEISE FÜR LEHRENDE & STUDIERENDE
VI – Giảng viên:
-
Hướng dẫn sinh viên cách dùng phép khử Gauss để nhận biết hạng
-
Dạy cả cách trực quan và đại số
-
Tích hợp bài toán thực tế như: mã hóa dữ liệu, mô phỏng vật lý
DE – Für Lehrende:
-
Gaussian-Elimination zur Bestimmung des Rangs lehren
-
Sowohl algebraisch als auch visuell erklären
-
Mit praktischen Beispielen aus Datenanalyse oder Simulationen arbeiten
VI – Sinh viên:
-
Đừng chỉ kiểm tra định thức – hãy hiểu tại sao điều đó quan trọng
-
Luyện nhiều ví dụ với ma trận 2 × 2, 3 × 3
-
Kết nối ma trận khả nghịch với nghiệm duy nhất của hệ phương trình
DE – Für Studierende:
-
Nicht nur Determinante prüfen – verstehen, warum das zählt
-
Viele Übungsbeispiele mit kleinen Matrizen rechnen
-
Zusammenhang mit eindeutigen Lösungen erkennen
LỜI KẾT | ABSCHLUSS
Khả nghịch không chỉ là thuộc tính của ma trận – đó là dấu hiệu của sự “hoàn chỉnh” trong ánh xạ tuyến tính. Ma trận khả nghịch là chìa khóa để giải hệ phương trình, bảo toàn thông tin và xây dựng nền tảng vững chắc cho đại số tuyến tính hiện đại.
facingX chúng tôi giúp bạn không chỉ nhận biết đâu là ma trận khả nghịch, mà còn học cách tư duy như một nhà toán học.
-
Giảng dạy song ngữ chuẩn quốc tế;
-
Nắm chắc nền tảng – hiểu sâu bản chất;
-
Kết nối học online với giảng viên chuyên ngành;
-
Đồng hành trên lộ trình du học từ Việt Nam ra thế giới.