Lineare Algebra - Đại số tuyến tính: Tuần 3 – Dạng bậc thang và phép khử Gauss / Stufenform & Gaußsches Eliminationsverfahren

GIỚI THIỆU | EINFÜHRUNG

VI – Tiếng Việt:

Sau khi đã hiểu về ma trận và các phép toán cơ bản, tuần này sinh viên sẽ học cách đưa một hệ phương trình tuyến tính về dạng đơn giản nhất – gọi là dạng bậc thang, thông qua một công cụ cực kỳ mạnh mẽ: Phép khử Gauss.

Đây là một kỹ thuật nền tảng trong Toán học ứng dụng, giúp giải hệ phương trình, tính hạng ma trận và xây dựng cơ sở cho nhiều thuật toán trong Tin học.

 

DE – Tiếng Đức:

Nach dem Verständnis von Matrizen und Grundoperationen lernen die Studierenden in dieser Woche, lineare Gleichungssysteme in Stufenform zu überführen, mithilfe eines mächtigen Werkzeugs: dem Gaußschen Eliminationsverfahren.

Dieses Verfahren ist grundlegend in der angewandten Mathematik, zur Lösung von LGS, zur Bestimmung des Rangs und als Basis vieler Algorithmen in der Informatik.

 

 KHÁI NIỆM | BEGRIFF

VI – Tiếng Việt:

• Dạng bậc thang (Row Echelon Form) là dạng ma trận có:

  1. Tất cả các hàng 0 nằm ở dưới cùng.

  2. Trong mỗi hàng, phần tử đầu tiên khác 0 (gọi là “pivot”) phải nằm bên phải pivot của hàng trên.

  3. Tất cả các phần tử dưới pivot đều bằng 0.

• Phép khử Gauss là quá trình biến đổi ma trận bằng các phép biến đổi sơ cấp hàng (row operations) để đưa về dạng bậc thang.

 

DE – Tiếng Đức:

• Stufenform (Zeilen-Stufenform) einer Matrix erfüllt:

  1. Alle Nullzeilen stehen unten.

  2. Das erste Nichtnull-Element (Pivot) jeder Zeile liegt rechts vom Pivot der vorherigen Zeile.

  3. Unterhalb jedes Pivots stehen nur Nullen.

• Gaußsches Eliminationsverfahren ist der Prozess, bei dem eine Matrix durch elementare Zeilenumformungen in Stufenform gebracht wird.

 

 Ý NGHĨA & ỨNG DỤNG | BEDEUTUNG & ANWENDUNG

VI – Tiếng Việt:

• Giải hệ phương trình tuyến tính nhanh, chính xác.

• Phát hiện hệ vô nghiệm hoặc có vô số nghiệm.

• Xác định hạng (rank) của ma trận.

• Là bước đầu trong các thuật toán tính nghịch đảo, định thức, phân tích LU.

 

DE – Tiếng Đức:

• Schnelle und präzise Lösung linearer Gleichungssysteme.

• Erkennung von Unlösbarkeit oder unendlich vielen Lösungen.

• Bestimmung des Rangs einer Matrix.

• Grundlage für weitere Verfahren wie Inverse, Determinante, LU-Zerlegung.

 

LƯU Ý CHO GIẢNG VIÊN VÀ SINH VIÊN | HINWEISE FÜR LEHRENDE UND STUDIERENDE

VI – Giảng viên:

• Giảng dạy theo mô hình trực quan (dùng mũi tên, đánh dấu pivot).

• Đừng chỉ đưa ra quy tắc – hãy lý giải vì sao lại cần đưa về dạng bậc thang.

• Liên hệ với thuật toán lập trình – khử Gauss là cơ sở của nhiều chương trình tính toán.

 

DE – Für Lehrende:

• Visualisierung durch Pfeile und Pivot-Markierungen.

• Nicht nur Regeln zeigen, sondern erklären: Warum Stufenform?

• Verbindungen zur Informatik herstellen – Gauß liegt vielen Algorithmen zugrunde.

 

VI – Sinh viên:

• Cẩn thận với sai sót trong phép biến đổi hàng (đặc biệt dấu ±).

• Nắm vững điều kiện kết thúc quá trình khử.

• Nên viết ra từng bước rõ ràng để tránh nhầm lẫn.

 

DE – Für Studierende:

• Achten Sie auf Vorzeichenfehler bei Zeilenumformungen.

• Verstehen, wann das Verfahren abgeschlossen ist.

• Alle Schritte sauber notieren – das reduziert Fehler.

 

 KHÓ KHĂN & GIẢI PHÁP | SCHWIERIGKEITEN & STRATEGIEN

Đối tượng	VI – Khó khăn	DE – Schwierigkeit	Giải pháp / Lösung
Giảng viên	Học viên dễ nản khi tính toán dài	Lange Rechnungen demotivieren	Dạy theo từng khối, phân tích trực quan
Sinh viên	Dễ sai ở bước rút gọn hàng	Fehler bei Zeilenreduktion	Làm chậm, luyện nhiều dạng đơn giản trước
Tất cả	Mất dấu pivot – dẫn tới sai toàn bộ	Pivot-Fehler führen zu falschem Ergebnis	Đánh dấu rõ từng pivot, dùng màu hoặc khung

 

 

 VÍ DỤ CỤ THỂ & GIẢI THÍCH | BEISPIEL MIT ERKLÄRUNG

VI – Tiếng Việt:

Giải hệ phương trình sau bằng khử Gauss:

 

Bước 1 – Viết ma trận mở rộng:

 

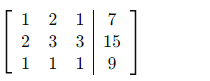
Bước 2 – Khử Gauss:

• R2 ← R2 − 2·R1

• R3 ← R3 − R1

 

Bước 3 – R3 ← R3 − R2:

 

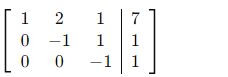
Bước 4 – Giải ngược từ dưới lên:

 

 

DE – Tiếng Đức:

Löse das folgende LGS mit dem Gauß-Verfahren:

 

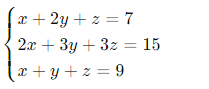
Schritt 1 – Erweiterte Matrix aufschreiben:

 

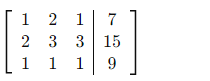
Schritt 2 – Zeilenoperationen:

• R2 ← R2 − 2·R1

• R3 ← R3 − R1

 

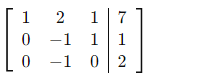
Schritt 3 – R3 ← R3 − R2:

 

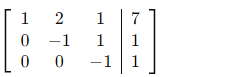
Schritt 4 – Rückwärtseinsetzen:

 LỜI KẾT | ABSCHLUSS

Phép khử Gauss là chiếc chìa khóa đầu tiên mở cánh cửa vào thế giới của các thuật toán đại số tuyến tính. Nó không chỉ giúp sinh viên giải các hệ phương trình một cách có hệ thống, mà còn rèn luyện tư duy logic, khả năng phân tích và tinh thần kiên trì – những phẩm chất đặc biệt quan trọng khi học tập tại môi trường đại học quốc tế.

 

Tại facingX.com, chúng tôi hiểu rõ những khó khăn mà sinh viên Việt Nam phải đối mặt trong năm đầu du học. Chính vì vậy, chúng tôi xây dựng các chương trình giảng dạy Toán tư duy và các môn học đại cương theo hướng song ngữ Việt – Đức/Anh, tích hợp cả lý thuyết – ví dụ – bài tập – hướng dẫn học hiệu quả.

 

Ngoài ra, với dịch vụ kết nối giảng dạy online toàn cầu, facingX giúp các bạn sinh viên đang học năm nhất tại Đức, Nhật, Úc, Canada, EU… luôn có được người đồng hành học thuật đáng tin cậy, ngay cả khi học từ xa.

 

facingX.com – Bệ phóng tri thức, kết nối toàn cầu cho sinh viên Việt Nam.

 

 

---