Không gian tuyến tính là một thế giới đa chiều, nhưng trong thế giới đó, có vô số không gian nhỏ hơn – gọi là không gian con.
GIỚI THIỆU | EINFÜHRUNG
VI – Tiếng Việt:
Không gian tuyến tính là một thế giới đa chiều, nhưng trong thế giới đó, có vô số không gian nhỏ hơn – gọi là không gian con. Bên cạnh đó, khái niệm độc lập tuyến tính giúp xác định tính “khác biệt” giữa các vectơ – tránh dư thừa, trùng lặp. Cùng nhau, hai khái niệm này giúp sinh viên nhận diện cấu trúc của hệ phương trình, ma trận và toàn bộ không gian dữ liệu.
DE – Tiếng Đức:
Ein Vektorraum enthält viele kleinere Strukturen – sogenannte Unterräume. Gleichzeitig erlaubt die lineare Unabhängigkeit, die Einzigartigkeit von Vektoren zu erkennen – und Redundanzen zu vermeiden. Beide Konzepte sind zentral, um Strukturen in Gleichungssystemen, Matrizen und Datensätzen zu verstehen.
KHÁI NIỆM CƠ BẢN | GRUNDLAGEN
VI – Tiếng Việt:

DE – Tiếng Đức:

Ý NGHĨA & VAI TRÒ | BEDEUTUNG & FUNKTION
VI – Tiếng Việt:
-
Không gian con là “hệ sinh thái nhỏ” trong không gian lớn – giúp phân tích dữ liệu, tối ưu hóa, kiểm tra nghiệm.
-
Độc lập tuyến tính cho biết tập vectơ có “bổ sung thông tin” hay không.
-
Hiểu hai khái niệm này giúp sinh viên phát hiện cấu trúc ẩn trong ma trận và hệ phương trình.
DE – Tiếng Đức:
-
Unterräume sind „kleine Welten“ im großen Raum – wichtig für Datenanalyse, Optimierung, Lösbarkeit.
-
Lineare Unabhängigkeit zeigt, ob Vektoren neue Informationen liefern.
-
Wer beides versteht, erkennt verborgene Strukturen in Matrizen und Gleichungssystemen.
LƯU Ý CHO GIẢNG VIÊN & SINH VIÊN | HINWEISE FÜR LEHRENDE & STUDIERENDE
VI – Giảng viên:
-
Dẫn dắt bằng trực giác hình học: mặt phẳng qua gốc tọa độ, đường thẳng, trục.
-
Phân tích mối liên hệ giữa không gian con và nghiệm của hệ phương trình.
-
Khuyến khích sinh viên tự kiểm tra điều kiện không gian con.
DE – Für Lehrende:
-
Geometrische Intuition aufbauen: Ebenen, Geraden durch den Ursprung.
-
Zusammenhang zwischen Unterräumen und Lösungsräumen betonen.
-
Studierende zur aktiven Überprüfung der Subraum-Bedingungen anregen.
VI – Sinh viên:
-
Dễ nhầm lẫn không gian con với tập con – cần nhớ 3 điều kiện.
-
Nên rèn luyện nhận biết tính độc lập tuyến tính qua ma trận.
-
Cố gắng vẽ hình – nhất là trong không gian 2D và 3D để hiểu bản chất.
DE – Für Studierende:
-
Verwechslungsgefahr: Unterraum ≠ beliebige Teilmenge → 3 Bedingungen beachten.
-
Lineare Unabhängigkeit durch Matrix-Methoden prüfen üben.
-
Visualisierung in R² & R³ hilft beim Verständnis.
VÍ DỤ CỤ THỂ & GIẢI THÍCH | BEISPIELE & ERKLÄRUNG
VI – Tiếng Việt:


DE – Tiếng Đức:

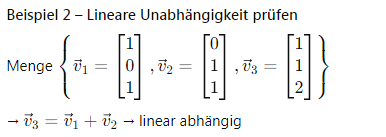
LỜI KẾT | ABSCHLUSS
Không gian con và độc lập tuyến tính giúp sinh viên “đọc vị” không gian – hiểu xem đâu là thông tin mới, đâu là dư thừa. Chúng là công cụ không thể thiếu để bước vào thế giới đại số trừu tượng, học máy và phân tích dữ liệu.
Tại facingX.com, chúng tôi giúp sinh viên làm chủ các khái niệm toán học khó thông qua:
Bài giảng song ngữ Việt – Đức/Anh rõ ràng, logic;
-
Ví dụ thực tế, trực quan dễ hiểu;
-
Nền tảng học trực tuyến – kết nối giảng viên và học viên quốc tế;
-
Hệ thống kiểm tra, luyện tập có phản hồi tự động;
-
Tư vấn chiến lược du học & chuẩn bị học thuật sớm từ Việt Nam.