Lineare Algebra - Đại số tuyến tính: Tuần 9 - Định thức: Định nghĩa và Tính chất / Determinanten: Definition & Eigenschaften

Tuần 9 – Định thức - Mảnh ghép then chốt của đại số tuyến tính / Die Determinante – Der Schlüssel zur Lösbarkeit

GIỚI THIỆU | EINFÜHRUNG

VI – Tiếng Việt:
Trong đại số tuyến tính, định thức không đơn thuần là một con số – nó là "dấu hiệu" của tính khả nghịch, là thước đo sự biến dạng không gian khi một ánh xạ tuyến tính tác động. Dù trông có vẻ kỹ thuật, định thức là công cụ xuất hiện khắp nơi: từ giải hệ phương trình, tính thể tích, đến xác định hướng quay của hình ảnh trong đồ họa 3D.

 

DE – Tiếng Đức:
In der linearen Algebra ist die Determinante weit mehr als eine Zahl – sie ist Indikator für Invertierbarkeit, Maß für die Raumverzerrung durch lineare Abbildungen und Werkzeug zur Lösung von Gleichungssystemen. Sie begegnet uns in Geometrie, Physik, Computergrafik und darüber hinaus.

 

 KHÁI NIỆM CƠ BẢN | GRUNDLAGEN

VI – Tiếng Việt:

1. Định thức là gì?
   Định thức là một giá trị vô hướng gán cho ma trận vuông.

   • Ký hiệu: det⁡(A) hoặc |A|

   • Với ma trận 2 × 2:

     

      

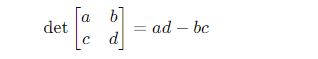
2. Ý nghĩa trực giác:

   • Trong hình học: định thức là diện tích (2D) hoặc thể tích (3D) của hình ảnh sau khi bị biến đổi bởi ma trận.

   • Nếu det⁡ (A) = 0 → ánh xạ làm "xẹp" không gian → ma trận không khả nghịch.

 

DE – Tiếng Đức:

1. Was ist die Determinante?
   Die Determinante ist ein Skalarwert, der einer quadratischen Matrix zugeordnet wird.

   • Notation: det⁡(A) oder |A|

   • Für eine 2 × 2 -Matrix:

     

      

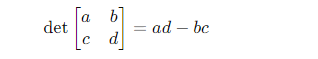
2. Intuitive Bedeutung:

   • Geometrisch: die Determinante beschreibt die Fläche (2D) oder das Volumen (3D) nach Transformation.

   • det⁡ (A) = 0 bedeutet: Raum kollabiert → Matrix ist nicht invertierbar.

 

TÍNH CHẤT CỦA ĐỊNH THỨC | EIGENSCHAFTEN DER DETERMINANTE

VI – Tiếng Việt:

DE – Tiếng Đức:

 

LƯU Ý CHO GIẢNG VIÊN & SINH VIÊN | HINWEISE FÜR LEHRENDE & STUDIERENDE

VI – Giảng viên:

• Tránh dạy định thức chỉ như “công thức tính máy móc”.

• Nên kết hợp hình học và đại số để giải thích trực quan.

• Tập trung vào bản chất: điều kiện để ma trận khả nghịch.

 

DE – Für Lehrende:

• Nicht nur als „Rezept“ vermitteln – sondern mit geometrischem Bezug.

• Verbindung zwischen Algebra und Visualisierung betonen.

• Fokus auf Invertierbarkeit und strukturelle Aussagekraft der Determinante.

 

VI – Sinh viên:

• Không cần học thuộc định nghĩa tổng quát định thức (theo hoán vị) ngay – nên tập trung vào định thức bậc 2, 3 và hiểu tính chất.

• Rèn kỹ năng áp dụng định thức để:

  • Kiểm tra tính khả nghịch

  • Tính thể tích

  • Giải hệ phương trình qua phương pháp Cramer

 

DE – Für Studierende:

• Zunächst keine Angst vor der allgemeinen Definition – mit kleinen Matrizen üben.

• Trainieren Sie:

  • Invertierbarkeit prüfen

  • Volumen berechnen

  • Cramersche Regel anwenden

 

VÍ DỤ CỤ THỂ & GIẢI THÍCH | BEISPIELE & ERKLÄRUNG

VI – Tiếng Việt:

 

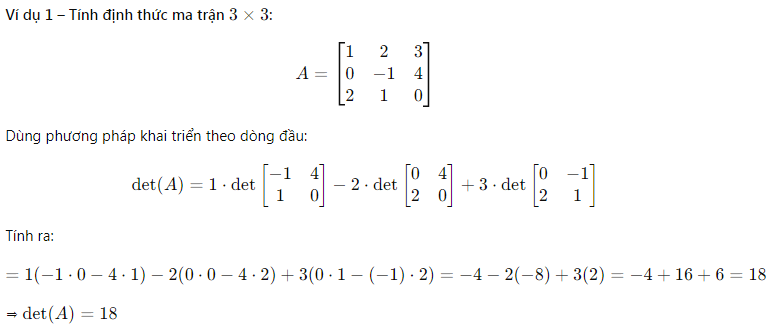
DE – Tiếng Đức:

 

 LỜI KẾT | ABSCHLUSS

Định thức là “một con số nhỏ với sức mạnh lớn” – giúp ta xác định khi nào không gian bị nén lại, khi nào hệ phương trình có nghiệm duy nhất, và khi nào một phép biến đổi là khả nghịch. Từ một biểu thức tưởng chừng chỉ là kỹ thuật, định thức mở ra cả thế giới ứng dụng sâu rộng trong khoa học, kỹ thuật và công nghệ.

 

facingX.com, chúng tôi giúp sinh viên Việt Nam nắm vững từng viên gạch nhỏ như định thức – để từng bước xây dựng nền tảng vững chắc cho hành trình du học quốc tế:

• Bài giảng song ngữ chất lượng cao – Việt – Đức/Anh;

• Phân tích sâu sắc, ứng dụng thực tiễn – từ đại số đến đời sống;

• Kết nối học viên và giảng viên qua lớp học online chuyên sâu;

• Lộ trình học thông minh, định hướng rõ ràng cho năm nhất.

facingX.com – Nơi bạn học Toán để bước vào thế giới.

 

---