Giải hệ phương trình tuyến tính – Cốt lõi của mọi mô hình đa biến

Giải hệ phương trình tuyến tính (Solving Linear Systems)

1. Mô tả tổng quan

Trong hành trình học Toán bậc phổ thông và đại học, đặc biệt ở các chương trình quốc tế như IB, A-level, hoặc đại học năm nhất tại các nước như Đức, Úc, Canada, việc giải hệ phương trình tuyến tính là một trong những kỹ năng nền tảng và thiết yếu nhất.

Hệ phương trình tuyến tính không chỉ là kiến thức lý thuyết thuần túy mà còn ứng dụng trong rất nhiều ngành học như Kỹ thuật, Kinh tế, Khoa học máy tính, Trí tuệ nhân tạo và cả trong các nghiên cứu xã hội. Khi hiểu rõ và giải được các hệ phương trình này, học sinh không chỉ thành thạo toán học mà còn xây dựng được tư duy logic, phân tích và giải quyết vấn đề hiệu quả.

2. Khái niệm cơ bản

Hệ phương trình tuyến tính là tập hợp gồm nhiều phương trình tuyến tính – mỗi phương trình là một biểu thức có dạng:

Trong đó:

• x1,x2,...,xn ​: là các ẩn số

• a1,a2,...,an ​: là các hệ số (số thực hoặc phức)

• b: là hằng số

Một hệ có thể gồm 2, 3 hoặc nhiều phương trình tùy bài toán. Nhiệm vụ của chúng ta là tìm giá trị của các ẩn số sao cho tất cả các phương trình trong hệ đều đúng.

 

3. Các nội dung chính yếu

a. Các phương pháp giải phổ biến:

• Phép thế (Substitution)

                     Dùng một phương trình để biểu diễn một biến theo các biến khác rồi thay vào phương trình còn lại.

                     Phù hợp với hệ nhỏ (2-3 ẩn).

• Phép cộng đại số (Elimination / Addition)

                    Biến đổi hệ sao cho một ẩn bị triệt tiêu, rút gọn dần cho đến khi tìm được lời giải.

• Phương pháp ma trận (Matrix method):

                     Dùng biến đổi ma trận hoặc định thức (determinant), Gauss hoặc Gauss-Jordan để giải.

                    Cần thiết khi làm việc với hệ phương trình lớn, thường được học trong Toán cao cấp.

• Phân tích Gauss (Gaussian Elimination)

                   Đưa hệ phương trình về dạng bậc thang (row echelon) bằng phép biến đổi sơ cấp trên các dòng của ma trận.
                   Sau đó giải bằng phép thế ngược từ dòng dưới lên trên.

• Sử dụng phần mềm / máy tính

                  MATLAB, Python (NumPy), hoặc máy tính cầm tay có thể giải nhanh hệ phương trình phức tạp.

                  Ví dụ: Trong Python với NumPy:

         import numpy as np

         A = np.array([[2, 3], [4, -1]])

         B = np.array([5, 11])

         X = np.linalg.solve(A, B) print(X)

                 → Công cụ bắt buộc phải biết nếu bạn là sinh viên khối kỹ thuật, khoa học máy tính hoặc kinh tế dữ liệu.

b. Phân loại lời giải:

• Hệ có nghiệm duy nhất

• Hệ vô nghiệm

• Hệ có vô số nghiệm

 

4. Ví dụ minh họa

Ví dụ 1 (Hệ 2 phương trình – 2 ẩn):

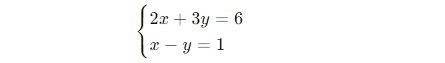
Giải bằng phương pháp thế:

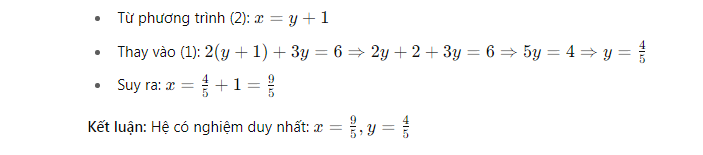
5. Những khó khăn thường gặp

• Không phân biệt được hệ có nghiệm – vô nghiệm – vô số nghiệm

            → Thiếu kiến thức về bậc thang dòng và hạng ma trận (rank)

• Không hiểu ý nghĩa hình học của bài toán
  → Dẫn đến học vẹt công thức, không áp dụng được

• Gặp sai sót khi biến đổi sơ cấp thủ công
  → Lỗi sai lan truyền, làm sai toàn bộ hệ

• Thiếu kỹ năng dùng phần mềm giải hệ lớn
  → Không biết viết code hoặc không dùng được Python/MATLAB

• Khi học bằng tiếng Anh (trong môi trường du học), có thể bị “choáng” bởi thuật ngữ như “row echelon form”, “pivot”, “rank”, “inverse matrix”...

 

6. Cách học hiệu quả

✔ Nắm chắc khái niệm cơ bản

Học sinh cần phân biệt rõ giữa hệ có nghiệm duy nhất, vô nghiệm và vô số nghiệm. Hiểu kỹ từng định nghĩa giúp tránh mắc lỗi tư duy về bản chất.

✔ Luyện tập đa dạng phương pháp

Đừng chỉ học một cách giải. Học sinh nên thử nhiều phương pháp trên cùng một hệ để hiểu sâu bản chất và tăng kỹ năng linh hoạt.

✔ Thực hành trên phần mềm

Với những bạn học các chương trình quốc tế, việc sử dụng phần mềm như Desmos, GeoGebra, MATLAB, hoặc viết code Python là kỹ năng cần thiết.

✔ Kết hợp học bằng tiếng Anh

Vì nội dung này được giảng dạy trong các chương trình quốc tế, học sinh nên làm quen với các từ vựng Toán học bằng tiếng Anh như:

• System of equations – hệ phương trình

• Solution set – tập nghiệm

• Consistent / inconsistent – hệ có / không có nghiệm

• Gaussian elimination – phương pháp khử Gauss

✔ Học với giáo viên giàu kinh nghiệm

Việc có người hướng dẫn giúp học sinh rút ngắn thời gian hiểu bài và tránh các lỗi sai thường gặp. Đặc biệt với những bạn chuẩn bị du học, giáo viên có thể mô phỏng đúng phong cách thi / kiểm tra của trường quốc tế.

 

7. Kết luận

Giải hệ phương trình tuyến tính là một kỹ năng cốt lõi, mở đầu cho nhiều lĩnh vực học thuật sau này. Nếu bạn đang chuẩn bị du học, hoặc đang học năm nhất tại nước ngoài và cảm thấy “đuối sức” , đừng ngần ngại – facingX giúp bạn giải hệ phương trình dễ như trở bàn tay

---