Đại số tuyến tính không chỉ là một môn học cơ bản – mà là ngôn ngữ chung của khoa học dữ liệu, trí tuệ nhân tạo và mô hình toán học hiện đại.
Tuần 1 – Mở cánh cửa Đại số tuyến tính / Einstieg in die Lineare Algebra
1.Giới thiệu | Einführung
VI – Tiếng Việt:
Đại số tuyến tính là môn học mở đầu cho hành trình tiếp cận tư duy trừu tượng của Toán học bậc đại học. Môn học này giúp sinh viên hiểu được các khái niệm nền tảng như hệ phương trình tuyến tính, vectơ, ma trận và ánh xạ tuyến tính – những yếu tố cốt lõi không chỉ trong Toán học mà còn trong các ngành như Khoa học máy tính, Kinh tế lượng và Trí tuệ nhân tạo.
DE – Tiếng Đức:
Lineare Algebra ist ein zentrales Grundlagenfach, das Studierenden den Einstieg in das abstrakte Denken der Hochschulmathematik ermöglicht. Es vermittelt grundlegende Konzepte wie lineare Gleichungssysteme, Vektoren, Matrizen und lineare Abbildungen – Schlüsselkomponenten nicht nur in der Mathematik, sondern auch in der Informatik, Ökonometrie und Künstlichen Intelligenz.

2. Mục tiêu bài học | Lernziele
VI – Tiếng Việt:
-
Làm quen với khái niệm hệ phương trình tuyến tính.
-
Biểu diễn bài toán thực tế bằng ma trận và vectơ.
-
Giải hệ phương trình đơn giản bằng phương pháp khử Gauss.
-
Phân biệt rõ các khái niệm: ẩn số, hệ số, nghiệm, ma trận, vectơ.
DE – Tiếng Đức:
-
Einführung in lineare Gleichungssysteme (LGS).
-
Darstellung von praktischen Problemen mittels Matrizen und Vektoren.
-
Lösung einfacher LGS durch Gaußsches Eliminationsverfahren.
-
Klare Unterscheidung von: Unbekannten, Koeffizienten, Lösung, Matrix, Vektor.
3. Kiến thức trọng tâm | Zentrale Inhalte
VI – Tiếng Việt:
- Hệ phương trình tuyến tính
Là tập hợp gồm nhiều phương trình có chung các ẩn, dạng:
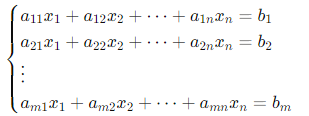
- Ma trận hệ số và vectơ hằng số
Có thể viết gọn lại dưới dạng ma trận:
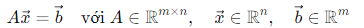
- Phương pháp khử Gauss (Gaussian Elimination)
-
Dùng các phép biến đổi sơ cấp hàng để đưa hệ về dạng bậc thang.
-
Từ đó giải ra các nghiệm từ dưới lên.
DE – Tiếng Đức:
- Lineares Gleichungssystem (LGS)
Eine Sammlung mehrerer Gleichungen mit denselben Unbekannten, z. B.:

- Koeffizientenmatrix und Ergebnisvektor
Kompakte Darstellung als:

- Gaußsches Eliminationsverfahren
-
Anwendung von elementaren Zeilenumformungen zur Stufenform.
-
Rückwärtseinsetzen zur Bestimmung der Lösung.
4. Ý nghĩa và vai trò | Bedeutung und Rolle
-
Trong toán học: Giải quyết cấu trúc đại số của không gian và ánh xạ.
In der Mathematik: Untersucht Strukturen von Räumen und linearen Abbildungen. -
Trong khoa học máy tính: Biểu diễn dữ liệu, giải bài toán tối ưu, lập trình hình học.
In der Informatik: Für Datenstrukturen, Optimierung und Geometrie unverzichtbar. -
Trong ứng dụng thực tế: Mô phỏng kỹ thuật, xử lý hình ảnh, mạng nơ-ron...
In der Praxis: Simulationen, Bildverarbeitung, neuronale Netze etc.
5. Lưu ý cho giảng viên và sinh viên | Hinweise für Lehrende und Studierende
Giảng viên cần chú ý:
-
Giảng giải rõ ràng mối liên hệ giữa thực tế và lý thuyết.
-
Không vội đi sâu vào định nghĩa hình thức – hãy dẫn dắt bằng ví dụ cụ thể.
-
Khuyến khích sinh viên diễn đạt bằng ngôn ngữ của chính họ (đặc biệt là sinh viên quốc tế).
Sinh viên cần chú ý:
-
Đừng học thuộc công thức – hãy hiểu bản chất bài toán.
-
Vẽ sơ đồ (mindmap) để hiểu các khái niệm như hệ, ma trận, nghiệm.
-
Tập thói quen viết lại bài bằng từ ngữ riêng của mình (bằng cả tiếng Việt & tiếng Đức).
6. Khó khăn thường gặp | Typische Schwierigkeiten
|
Đối tượng |
Khó khăn (VI) |
Schwierigkeit (DE) |
|---|---|---|
|
Giảng viên |
Giải thích khái niệm "hệ tuyến tính" quá trừu tượng |
Abstrakte Erklärung der LGS ohne Anwendung |
|
Sinh viên quốc tế |
Rào cản thuật ngữ và ký hiệu toán học tiếng Đức |
Sprachliche & symbolische Barrieren |
|
Tất cả |
Không biết phân biệt giữa ma trận, vectơ và hệ |
Verwechslung von Matrizen, Vektoren und Gleichungssystemen |
7. Chiến lược giảng dạy và học hiệu quả | Erfolgreiche Lernstrategie
-
Từ ví dụ → rút ra khái niệm → khái quát định nghĩa.
Vom Beispiel → zur Begriffserklärung → zur allgemeinen Definition. -
Dạy song song hai ngôn ngữ (tiếng Đức – tiếng Việt) giúp ghi nhớ sâu hơn.
-
Mỗi buổi học nên có một bài toán thực tế (ví dụ tính giá tiền theo số lượng hàng hóa) rồi biểu diễn lại thành hệ phương trình.
8. Ví dụ minh họa | Beispielaufgabe
VI – Tiếng Việt:
Một khách hàng mua 2 sản phẩm A và 3 sản phẩm B với tổng giá 16€.
Một người khác mua 1 sản phẩm A và 2 sản phẩm B với tổng giá 11€.
Hỏi giá mỗi sản phẩm.
Lập hệ:
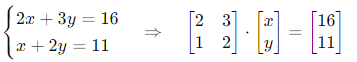
Giải ra được x = −1, y = 6 → nghiệm không hợp lý thực tế → cần kiểm tra lại dữ kiện.
DE – Tiếng Đức:
Ein Kunde kauft 2 Stück Produkt A und 3 Stück Produkt B für insgesamt 16 €.
Ein anderer Kunde kauft 1 Stück A und 2 Stück B für 11 €.
Was kostet jedes Produkt?
Gleichungssystem:
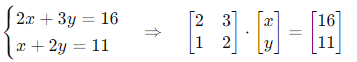
Lösung: x = −1, y = 6 → ökonomisch nicht sinnvoll → Eingabefehler prüfen.
Lời kết | Abschlussgedanken
Bắt đầu từ những hệ phương trình đơn giản, sinh viên sẽ dần tiếp cận một thế giới toán học trừu tượng và đầy ứng dụng thực tiễn.
Với một nền tảng vững chắc về đại số tuyến tính, các bạn không chỉ có thể hiểu được các thuật toán trong khoa học dữ liệu, trí tuệ nhân tạo, mà còn phát triển tư duy logic – một trong những kỹ năng sống còn khi học tập và làm việc trong môi trường học thuật quốc tế.
Tại facingX.com, chúng tôi tin rằng hành trình du học không chỉ là đi xa về khoảng cách địa lý, mà là sự tiến xa về tri thức, kỹ năng và tư duy toàn cầu.
Từ việc dạy ngoại ngữ chuẩn bị du học, đến kết nối giảng dạy online giữa giáo viên và học viên toàn cầu, và đặc biệt là những chương trình học thuật song ngữ như Đại số tuyến tính, chúng tôi mong muốn đồng hành cùng các bạn sinh viên trong những năm học đầu đời – nơi những viên gạch đầu tiên của tương lai được đặt xuống.