Tuần 1: Giới thiệu về Giải tích / Einführung in die Analysis của môn học Toán Giải tích 1, gồm 3 phần: Tư duy toán học đại học – Tập hợp số – Số thực. Bài giảng được viết song ngữ Việt – Đức
Tuần 1 – Giới thiệu về Giải tích / Einführung in die Analysis
(Bài giảng tổng hợp gồm 3 phần: Tư duy toán học đại học – Tập hợp số – Số thực)
1. Giới thiệu / Einführung
VI – Tiếng Việt:
Giải tích (Analysis) là một nhánh của toán học nghiên cứu về giới hạn, sự liên tục, đạo hàm và tích phân. Đây là nền tảng cho nhiều lĩnh vực khoa học và kỹ thuật – đặc biệt là vật lý, tin học, và kinh tế. Ở đại học Đức, môn Giải tích không chỉ dừng lại ở tính toán, mà còn tập trung vào tính chính xác, logic chặt chẽ và cách trình bày toán học theo tiêu chuẩn học thuật.
DE – Tiếng Đức:
Die Analysis ist ein Teilgebiet der Mathematik, das sich mit Grenzwerten, Stetigkeit, Ableitungen und Integralen beschäftigt. Sie bildet die Grundlage für viele naturwissenschaftliche und technische Disziplinen – insbesondere Physik, Informatik und Wirtschaft. In der Universität liegt der Fokus nicht nur auf Rechnen, sondern auf mathematischer Strenge, Logik und sauberer Beweisführung.

2. Ý nghĩa và vai trò của Giải tích / Bedeutung der Analysis
VI – Tiếng Việt:
-
Tư duy logic và khái niệm chuẩn mực: Giúp sinh viên học cách suy nghĩ chặt chẽ, từ định nghĩa đến hệ quả.
-
Nền tảng cho lập trình khoa học: Tư duy giới hạn và đạo hàm là cơ sở cho các thuật toán mô phỏng, đồ họa, AI.
-
Công cụ ứng dụng trong thực tiễn: Giải tích giúp mô hình hóa hiện tượng vật lý (tốc độ, gia tốc), tối ưu hóa trong kinh tế, xử lý tín hiệu số...
DE – Tiếng Đức:
-
Logisches Denken und exakte Begriffsbildung: Studierende lernen, sauber und präzise zu argumentieren.
-
Grundlage für wissenschaftliches Programmieren: Grenzwerte und Ableitungen sind essenziell für Simulationen, Computergrafik und KI.
-
Anwendungen in der Praxis: Analysis wird verwendet zur Modellierung physikalischer Prozesse, zur Optimierung in der Wirtschaft oder zur digitalen Signalverarbeitung.
3. Tư duy toán học đại học ở Đức – Mathematisches Denken an der Uni
Giới thiệu
VI:
Ở bậc đại học, đặc biệt tại Đức, toán học không chỉ là tìm kết quả đúng mà còn là chứng minh đúng, giải thích rõ, và trình bày chặt chẽ.
DE:
In der Universität – besonders in Deutschland – geht es in der Mathematik nicht nur um das richtige Ergebnis, sondern auch um korrekte Beweise, klare Argumentation und formale Darstellung.
Khái niệm chính
|
Thuật ngữ |
Giải thích (VI) |
Erklärung (DE) |
|---|---|---|
|
Định nghĩa |
Cách mô tả chính xác khái niệm |
Genaue Beschreibung eines Begriffs |
|
Định lý (Satz) |
Kết quả được chứng minh |
Mathematische Aussage mit Beweis |
|
Chứng minh |
Lý lẽ dẫn đến kết luận |
Logische Herleitung des Satzes |
Ý nghĩa
-
Xây dựng nền tảng tư duy logic cho các môn học tiếp theo.
-
Là kỹ năng bắt buộc trong thi cử, nghiên cứu và viết luận toán.
-
Làm quen cách học theo kiểu "hiểu tại sao", thay vì chỉ "làm sao".
Lưu ý cho giảng viên & sinh viên
|
Giảng viên |
Sinh viên |
|---|---|
|
Tập trung giảng định nghĩa trước công thức |
Đừng nhảy vào làm bài khi chưa hiểu khái niệm |
|
Nêu ví dụ phản ví dụ khi dạy định lý |
Ghi chép bằng tiếng Đức + diễn đạt lại bằng tiếng Việt |
|
Sử dụng hình ảnh, sơ đồ trong giảng khái niệm trừu tượng |
Tập viết lời giải có đầy đủ giải thích |
Ví dụ 1: Trình bày lời giải toán học kiểu đại học
❓ Câu hỏi: Toán học đại học khác gì toán phổ thông?
VI:
Phổ thông:
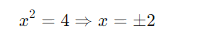
→ Xong, không cần giải thích thêm.
Đại học:

DE:
In der Schule:
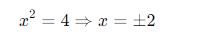
→ Fertig, keine weitere Begründung nötig.
An der Uni:

→ Trình bày có lập luận, theo tiêu chuẩn học thuật.
2. Nhắc lại tập hợp số – Wiederholung der Zahlmengen
Giới thiệu
VI:
Tập hợp số là nền tảng để xây dựng các khái niệm về giới hạn, đạo hàm. Việc phân biệt các loại số giúp xác định phạm vi áp dụng của các định lý.
DE:
Zahlmengen sind die Grundlage der Analysis. Ihre genaue Kenntnis hilft beim Anwenden mathematischer Sätze.
Khái niệm & ký hiệu
|
Ký hiệu |
Tiếng Việt |
Deutsch |
Ví dụ |
|---|---|---|---|
|
N |
Số tự nhiên |
natürliche Zahlen |
0, 1, 2, 3, ... |
|
Z |
Số nguyên |
ganze Zahlen |
-3, 0, 5 |
|
Q |
Số hữu tỉ |
rationale Zahlen |
1/2, -4/3 |
|
R |
Số thực |
reelle Zahlen |
π, sqrt{2}, −1 |
Ý nghĩa
-
Giúp xác định miền xác định của hàm số.
-
Phân biệt được loại số để áp dụng định lý đúng (VD: định lý chỉ áp dụng với Q hoặc R).
-
Tập hợp số cũng được dùng khi xét tính hội tụ trong giới hạn.
Ví dụ 2: Phân loại tập hợp số / Klassifizierung von Zahlenmengen
VI – Tiếng Việt:
Cho các số sau:
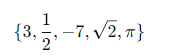
Phân loại:
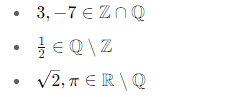
DE – Tiếng Đức:
Gegeben sind die Zahlen:
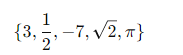
Einteilung:
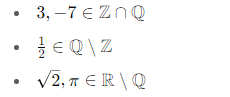
→ Kết luận / Fazit: Không phải số thực nào cũng là số hữu tỉ, và số vô tỉ xuất hiện thường xuyên trong Giải tích.
3. Số thực – Thứ tự và tính liên tục / Reelle Zahlen – Ordnung & Stetigkeit
Giới thiệu
VI:
Số thực không chỉ là "dãy số" kéo dài vô tận, mà còn có cấu trúc thứ tự tuyến tính và tính liên tục, khác hẳn với số hữu tỉ. Đây là đặc điểm then chốt trong Giải tích.
DE:
Reelle Zahlen haben eine lineare Ordnung und sind vollständig stetig – das unterscheidet sie wesentlich von den rationalen Zahlen.
Khái niệm chính
|
Khái niệm |
Giải thích (VI) |
Erklärung (DE) |
|---|---|---|
|
Thứ tự toàn phần |
Mọi cặp số thực đều so sánh được |
Jede zwei reelle Zahlen sind vergleichbar |
|
Không có “lỗ hổng” |
Bất kỳ khoảng nào cũng có số thực nằm trong |
Reelle Zahlen enthalten alle Grenzwerte – ohne Lücken |
Ý nghĩa trong Giải tích
-
Đảm bảo rằng giới hạn tồn tại thì kết quả vẫn là số thực.
-
Cho phép định nghĩa liên tục, đạo hàm, tích phân dựa trên tính liền mạch.
-
Tạo nền tảng cho các định lý: trung gian, Bolzano, định lý giới hạn.
Ví dụ 3: Tính liền mạch của số thực / Stetigkeit der reellen Zahlen
VI – Tiếng Việt: Hãy thử tìm một số hữu tỉ x∈Q sao cho:
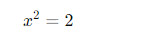
→ Không có số hữu tỉ nào thỏa điều kiện trên.
Tuy nhiên, trong R, tồn tại:
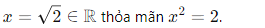
→ Điều này cho thấy số thực không bị đứt đoạn, có tính liên tục.
DE – Tiếng Đức:
Man versucht, eine rationale Zahl x∈Q, sodass
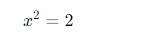
→ Es gibt keine rationale Zahl, die diese Bedingung erfüllt.
Aber in R existiert:
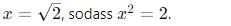
→ Das zeigt, dass die reellen Zahlen lückenlos und stetig sind.
Tổng kết bài học – Zusammenfassung
|
Nội dung chính đã học |
Kỹ năng đạt được |
|---|---|
|
Tư duy toán đại học |
Hiểu vai trò của định nghĩa, chứng minh |
|
Các tập hợp số |
Phân biệt rõ N,Z,Q,R |
|
Cấu trúc số thực |
Nhận biết tính thứ tự và liên tục của R |
Ghi chú cho giảng viên / Hinweise für Dozent:innen
-
Nên sử dụng mô phỏng trực quan (Geogebra, Desmos hoặc tay vẽ bảng) để giúp học viên hình dung.
-
Khuyến khích học viên tự đặt ví dụ đời thường liên quan đến giới hạn, đạo hàm, tích phân.
-
Nhấn mạnh: "Toán đại học không giống toán phổ thông" – chuyển từ kỹ thuật giải bài sang tư duy khái niệm.
Kết luận:
“Toán học đại học là hành trình từ việc biết kết quả sang hiểu vì sao kết quả đó tồn tại.” Và facingX đồng hành cùng bạn đi từ “Rechnen” đến “Beweisen”.