Tuần này sinh viên sẽ tiếp cận những định lý quan trọng nhất trong giải tích vi phân: định lý trung bình, định lý Rolle, định lý Lagrange, và định lý Fermat.
1. Giới thiệu – Einführung
VI – Tiếng Việt:
Sau khi nắm được khái niệm đạo hàm và cách khảo sát hàm số, tuần này sinh viên sẽ tiếp cận những định lý quan trọng nhất trong giải tích vi phân: định lý trung bình, định lý Rolle, định lý Lagrange, và định lý Fermat. Đây là những công cụ nền tảng toán học không chỉ để chứng minh mà còn để giải thích các hiện tượng thực tế: từ xác định cực trị, tối ưu hóa trong kinh tế, cho đến ứng dụng trong kỹ thuật và dữ liệu.
DE – Tiếng Đức:
Nachdem die Studierenden das Ableitungs-Konzept und die Kurvendiskussion gemeistert haben, lernen sie nun die zentralen Sätze der Differentialrechnung kennen: den Satz von Rolle, den Mittelwertsatz, den Satz von Lagrange und den Satz von Fermat. Diese sind nicht nur mathematisch bedeutsam, sondern auch praxisrelevant – in Wirtschaft, Technik oder Statistik.
2. Các định lý đạo hàm quan trọng – Wichtige Ableitungssätze
2.1. Định lý Rolle – Satz von Rolle
VI:
Nếu hàm số f liên tục trên đoạn [a,b], khả vi trên khoảng (a,b) và f(a) = f(b), thì tồn tại ít nhất một c ∈ (a,b) sao cho f′(c) = 0.
→ Ý nghĩa: tại một điểm giữa, hàm có tiếp tuyến nằm ngang.
DE:
Wenn fff stetig auf [a,b] und differenzierbar auf (a,b) ist und f(a) = f(b), dann existiert mindestens ein Punkt c ∈ (a,b), sodass f′(c) = 0.
→ Geometrisch: Die Funktion hat an einer Stelle eine waagerechte Tangente.
2.2. Định lý Lagrange – Satz von Lagrange (Mittelwertsatz)
VI:

DE:

2.3. Định lý Fermat – Satz von Fermat (Cực trị nội tại)
VI:

DE:

3. Ý nghĩa và ứng dụng – Bedeutung & Anwendungen
|
Ứng dụng thực tế |
Ý nghĩa toán học |
|---|---|
|
Tìm điểm cực đại/lợi nhuận tối ưu trong kinh tế |
Dựa vào định lý Fermat và đạo hàm |
|
Dự đoán xu hướng tăng giảm |
Nhờ Lagrange phát hiện vị trí thay đổi tốc độ |
|
Mô phỏng chuyển động vật lý |
Rolle thể hiện điểm đổi chiều tốc độ |
|
Chứng minh phương trình có nghiệm |
Dựa vào Rolle hoặc Lagrange kết hợp liên tục |
4. Ví dụ cụ thể – Konkrete Beispiele mit Erklärung
Ví dụ 1 – Áp dụng định lý Rolle
VI:
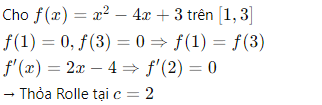
DE:
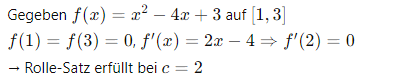
Ví dụ 2 – Lagrange: tốc độ trung bình và đạo hàm
VI:
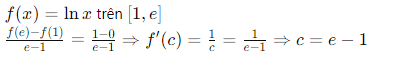
DE:
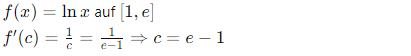
5. Khó khăn thường gặp – Typische Schwierigkeiten
Giảng viên:
|
Vấn đề |
Cách dạy hiệu quả |
|---|---|
|
Sinh viên thuộc định lý nhưng không hiểu ý nghĩa |
Diễn giải hình học, gắn với ví dụ chuyển động thực tế |
|
Quên điều kiện áp dụng |
Dạy sinh viên kiểm tra liên tục, khả vi, giá trị đầu cuối trước |
|
Học vẹt phát biểu |
Dạy qua hình minh họa + phân tích từng từ trong định nghĩa |
Sinh viên:
|
Khó khăn |
Cách học hiệu quả |
|---|---|
|
Lẫn lộn giữa Rolle và Lagrange |
So sánh song song: cùng điều kiện, khác kết luận |
|
Không hiểu ứng dụng thực tiễn |
Gắn với tối ưu hoá chi phí, chuyển động, tốc độ |
|
Ngại chứng minh |
Bắt đầu với ví dụ cụ thể rồi mới tổng quát hoá định lý |
6. Kết luận – Zusammenfassung
VI – Tiếng Việt:
Các định lý đạo hàm không chỉ là công cụ hình thức – mà là những chiếc cầu nối tư duy, giúp sinh viên vượt qua "học thuộc" để đi đến hiểu sâu và ứng dụng được. Với vai trò quan trọng trong tối ưu hóa, mô hình hóa và giải thích hành vi hàm số, những định lý như Rolle, Lagrange hay Fermat là nền tảng để sinh viên tiếp cận các ngành học hiện đại như kỹ thuật, kinh tế, khoa học dữ liệu.
DE – Tiếng Đức:
Die Ableitungssätze sind nicht nur formale Werkzeuge – sie sind Schlüssel zum tieferen Verständnis mathematischer Zusammenhänge. Ob in der Optimierung, Bewegungsanalyse oder Datenwissenschaft – Sätze wie Rolle, Lagrange oder Fermat sind essenziell.
Tại facingX.com, chúng tôi giúp các bạn sinh viên – đặc biệt là du học sinh năm nhất – tiếp cận các định lý này một cách trực quan, ứng dụng, thông minh. Không chỉ là bài giảng, chúng tôi mang đến một hệ sinh thái học tập toàn diện, bao gồm:
-
Tư vấn du học tại Đức, EU, Nhật, Úc, Canada
-
Dạy ngoại ngữ học thuật chuẩn bị cho môi trường đại học
-
Giảng dạy Toán tư duy – nền tảng cho mọi ngành kỹ thuật và công nghệ
-
Kết nối giảng viên và học viên trực tuyến, giúp học tập hiệu quả từ bất kỳ đâu