Toán Giải tích 1 – Mathematik 1 / Analysis 1: Tuần 9 – Nguyên hàm / Stammfunktionen: Bước đầu của tích phân

1. Giới thiệu – Einführung

VI – Tiếng Việt:
Sau khi tìm hiểu sâu về đạo hàm, ta quay lại câu hỏi ngược lại: Nếu biết đạo hàm, có tìm được hàm ban đầu không? Đó chính là khái niệm nguyên hàm. Việc tìm nguyên hàm là bước đầu tiên trong giải tích tích phân – mở ra ứng dụng rộng rãi trong hình học, vật lý, kinh tế và xử lý tín hiệu.

 

DE – Tiếng Đức:
Nachdem wir uns intensiv mit Ableitungen beschäftigt haben, stellen wir nun die Gegenfrage: Kann man aus der Ableitung die ursprüngliche Funktion rekonstruieren? Genau das ist die Idee der Stammfunktion. Die Bestimmung von Stammfunktionen ist der erste Schritt zur Integralrechnung – mit breiten Anwendungen in Geometrie, Physik, Ökonomie und Signalverarbeitung.

 

 2. Khái niệm – Definition

VI:
Cho một hàm số f(x), một hàm F(x) được gọi là nguyên hàm (stammfunktion) của f(x) nếu: F′(x) = f(x)

Ký hiệu nguyên hàm của f(x): ∫ f(x) dx = F(x)+C, với C ∈ R là hằng số tích phân.

 

DE:
Eine Funktion F(x) heißt Stammfunktion von f(x), wenn gilt: F′(x) = f(x)

Das unbestimmte Integral wird geschrieben als: ∫ f(x) dx = F(x)+C, wobei C ∈ R die Integrationskonstante ist.

 

 3. Ý nghĩa & Vai trò – Bedeutung und Rolle

Ứng dụng	Ý nghĩa
Tính diện tích dưới đường cong	Dựng từ nguyên hàm rồi áp dụng định lý cơ bản tích phân
Mô hình hoá chuyển động	Từ vận tốc → vị trí, từ gia tốc → vận tốc
Phân tích tín hiệu & xác suất	Sử dụng hàm phân phối tích lũy (CDF) là nguyên hàm của mật độ xác suất (PDF)
Phát triển giải tích nâng cao	Là nền tảng cho tích phân xác định, chuỗi Fourier, phương trình vi phân

 

4. Giảng viên & Sinh viên cần lưu ý – Hinweise für Lehrende & Lernende

Giảng viên:

Vấn đề cần chú ý	Gợi ý
Sinh viên bị lệch từ tư duy đạo hàm sang ngược lại	Làm rõ tính “ngược lại” và giới thiệu bằng các cặp hàm đã quen thuộc
Quá tập trung công thức, ít hiểu bản chất	Ưu tiên dạy qua hình học và chuyển động: vị trí từ vận tốc
Gây nhàm chán do quá cơ học	Kết hợp trò chơi công thức – tìm cặp nguyên hàm – đạo hàm tương ứng

 

Sinh viên:

 

5. Ví dụ cụ thể – Konkrete Beispiele mit Erklärung

Ví dụ 1 – Nguyên hàm đa thức / Stammfunktion eines Polynoms

VI

 

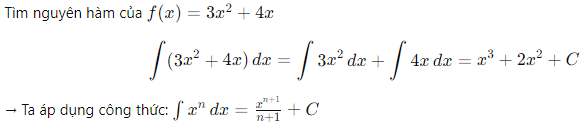
DE:

 

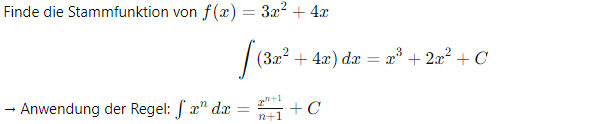
Ví dụ 2 – Hàm lượng giác / Trigonometrische Funktion

VI:

Giải thích: Lấy đạo hàm của sin⁡ x là cos ⁡x , nên ∫ cos⁡x dx = sinx + C

 

DE:

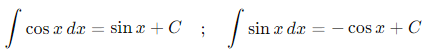
→ Ableitung von sin⁡x ist cos⁡x, daher Rückschluss durch Integration.

 

 6. Kết luận – Zusammenfassung

VI – Tiếng Việt:
Nguyên hàm là cánh cửa dẫn vào thế giới của tích phân – và cũng là cầu nối giữa đạo hàm và ứng dụng thực tiễn. Nắm vững nguyên hàm giúp sinh viên hiểu sâu bản chất của chuyển động, biến thiên và các bài toán tối ưu hoá trong đời sống thực. Đặc biệt, trong bối cảnh học đại học quốc tế, tư duy "ngược" và khả năng thao tác toán học linh hoạt là điểm mạnh vượt trội.

 

DE – Tiếng Đức:
Die Stammfunktion ist das Tor zur Integralrechnung – und zugleich die Brücke zwischen Ableitung und realen Anwendungen. Wer die Stammfunktionen versteht, begreift Bewegung, Veränderung und Optimierungsprozesse im Detail. Gerade im internationalen Studium ist diese Fähigkeit ein großer Vorteil.

 

Tại facingX.com, chúng tôi giúp sinh viên năm nhất – đặc biệt là du học sinh tại Đức và các nước EU – học Giải tích theo cách hệ thống, dễ hiểu, và gắn với các ứng dụng thực tế.
Nền tảng của chúng tôi không chỉ cung cấp bài giảng, mà còn kết nối bạn với:

• Tư vấn du học tại Đức, Nhật, Úc, Canada, EU

• Khóa học ngoại ngữ học thuật để sẵn sàng du học

• Lộ trình Toán tư duy từ cơ bản đến nâng cao

• Giảng dạy online với giáo viên chuyên ngành, hỗ trợ bạn học từ bất kỳ nơi đâu trên thế giới

facingX giúp bạn học hiệu quả từ gốc – chinh phục kiến thức toàn cầu.

 

---