Tuần học này chính là thời điểm “chuyển đổi tư duy” từ dãy số sang hàm số – từ tiến dần tới điểm đến việc xét đường đi có bị đứt quãng không.
1. Giới thiệu – Einführung
VI – Tiếng Việt:
Từ dãy số và giới hạn, sinh viên giờ đây bước sang một đối tượng mới: hàm số – mô hình toán học mô tả mối quan hệ đầu vào – đầu ra. Bài học tuần này mở ra khái niệm trung tâm: tính liên tục của hàm số, nền tảng cho đạo hàm, tích phân và mọi mô hình tính toán hiện đại.
DE – Tiếng Đức:
Nach Zahlenfolgen und Grenzwerten wenden wir uns jetzt dem zentralen Objekt der Analysis zu: Funktionen – mathematische Modelle für Eingabe-Ausgabe-Beziehungen. Die Stetigkeit ist das Herzstück dieser Woche – eine notwendige Voraussetzung für Ableitungen, Integrale und numerische Modellierungen.

2. Các khái niệm trọng tâm – Zentrale Begriffe
2.1. Hàm số – Funktion
|
Ký hiệu |
Giải thích (VI) |
Erklärung (DE) |
|---|---|---|
|
f: A → B |
Hàm f ánh xạ từ tập A sang B |
Funktion f ordnet jedem x ∈ A ein f (x) ∈ B zu |
|
x ↦ f (x) |
Biến đầu vào x, đầu ra là f (x) |
Zuordnung von Eingabe x zu Ausgabe f (x) |
2.2. Liên tục tại điểm – Stetigkeit an einem Punkt
Định nghĩa (VI):
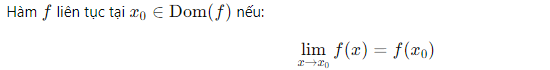
→ Không có “nhảy bước”, không “đứt đoạn”.
Definition (DE):
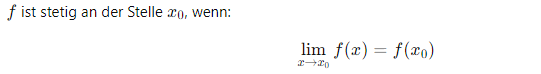
→ Kein Sprung, keine Lücke.
2.3. Tính liên tục trên tập – Stetigkeit auf einer Menge
|
Điều kiện |
Ý nghĩa (VI) |
Bedeutung (DE) |
|---|---|---|
|
f liên tục trên [a, b] |
Liên tục tại mọi điểm x ∈ [a, b] |
Stetig für alle x ∈ [a, b] |
|
Hàm không liên tục |
Có điểm gián đoạn |
Funktion hat Unstetigkeitsstelle |
3. Ý nghĩa – Warum ist das wichtig?
-
Liên tục = Không gián đoạn, mô hình hóa nhiều hiện tượng vật lý, sinh học, kinh tế.
-
Cần thiết để định nghĩa đạo hàm, tích phân – hai cột trụ của Giải tích.
-
Trong ngành CNTT & Data Science: mô hình học máy, tối ưu hoá đều giả định liên tục.
4. Ví dụ cụ thể có giải thích – Konkrete Beispiele mit Erklärung
Ví dụ 1
VI:

→ Mọi giá trị đầu vào "trượt" mượt mà → không nhảy, không gián đoạn.
DE:

→ Glatt, ohne Sprung – klassisches Beispiel stetiger Funktion.
Ví dụ 2 – Hàm không liên tục
VI:
Xét:

→ Không liên tục tại x = 0:

DE:
Betrachte:
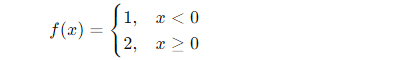
→ Nicht stetig bei x = 0:

Ví dụ 3 – Tính liên tục và đồ thị
VI:
Đồ thị của hàm liên tục không bị đứt đoạn. Ví dụ:
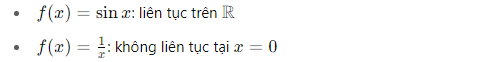
DE:
Graphen stetiger Funktionen haben keinen Sprung.
Beispiele:

5. Khó khăn thường gặp – Typische Schwierigkeiten
Đối với giảng viên:
|
Thách thức |
Gợi ý khắc phục |
|---|---|
|
Sinh viên nhầm lẫn giữa “liên tục” và “đều đặn” |
Dùng ví dụ có đồ thị “nhọn”, “gấp khúc” nhưng vẫn liên tục |
|
Chưa quen giải thích bằng định nghĩa lim f (x) = f (x0) |
Tập trung vào các ví dụ đơn giản có biểu diễn hình học rõ ràng |
|
Ngôn ngữ toán học khô khan |
Sử dụng kết hợp slide minh họa + hoạt động nhóm phân tích đồ thị |
Đối với sinh viên:
|
Vấn đề thường gặp |
Cách khắc phục |
|---|---|
|
Nhầm liên tục với đạo hàm |
Vẽ đồ thị minh họa sự liên tục nhưng không khả vi |
|
Không biết chứng minh liên tục như thế nào |
Làm từng bước: Tính giới hạn trái – phải → so sánh với f (x0) |
|
Bỏ qua định nghĩa, chỉ nhìn đồ thị |
Rèn kỹ năng diễn đạt định nghĩa bằng lời trước khi làm bài |
6. Kết luận – Zusammenfassung
VI – Tiếng Việt:
Tuần học này chính là thời điểm “chuyển đổi tư duy” từ dãy số sang hàm số – từ tiến dần tới điểm đến việc xét đường đi có bị đứt quãng không. Tính liên tục không chỉ là định nghĩa lý thuyết, mà là cốt lõi cho mọi ngành học kỹ thuật, khoa học máy tính, tài chính, và kinh tế học. Để làm chủ Giải tích, sinh viên phải hiểu rằng: không có liên tục → không có đạo hàm, không có mô hình hiện đại.
DE – Tiếng Đức:
Diese Woche markiert den Übergang von Folgen zu Funktionen, vom Punktdenken zur kontinuierlichen Bewegung. Die Stetigkeit ist nicht nur eine mathematische Definition, sondern das Fundament moderner Wissenschaft – von Physik bis Finanzmodellierung. Wer die Analysis beherrschen will, muss erkennen: Ohne Stetigkeit gibt es keine Ableitung, kein Modell, keine Kontrolle.
facingX giúp du học sinh xây nền móng vững chắc, sẵn sàng bứt phá trong học thuật và nghề nghiệp tại Đức.