Định thức – Chìa khóa xác định tính khả nghịch và cấu trúc không gian

Định thức – Chìa khóa xác định tính khả nghịch và cấu trúc không gian

1. Mô tả tổng quan

Định thức là một khái niệm tưởng như “kỹ thuật” nhưng thực chất lại đóng vai trò rất sâu sắc trong Đại số tuyến tính. Nó là chỉ số đặc trưng giúp bạn biết một ma trận có khả nghịch hay không, hệ phương trình có nghiệm duy nhất không, hay không gian có bị "ép dẹt" (suy biến) hay không.

Trong thực tế, định thức xuất hiện trong:

• Việc giải hệ phương trình tuyến tính (phương pháp Cramer)

• Kiểm tra tính độc lập tuyến tính

• Tính thể tích trong không gian nhiều chiều

• Các mô hình vật lý, kinh tế, cơ học, v.v.

Nắm vững định thức là bước đệm để bạn hiểu sâu hơn các khái niệm trừu tượng như: không gian con, ánh xạ tuyến tính, chéo hóa, giá trị riêng (eigenvalues)...

 

2. Khái niệm và nội dung chính cần nắm

✅ Định thức là gì?

Định thức (determinant) là một giá trị số duy nhất được tính từ một ma trận vuông.
Ký hiệu:

• det⁡(A) hoặc |A|

Về bản chất:

• Nếu det(A)=0 → Ma trận suy biến, không thể nghịch đảo

• Nếu det⁡(A)≠0 → Ma trận khả nghịch, không gian được bảo toàn

Hiểu đơn giản: định thức đo mức độ “biến dạng thể tích” mà một ánh xạ tuyến tính gây ra. Nếu định thức bằng 0 → toàn bộ không gian bị “xẹp xuống” (dẹt).

 

3. Cách tính định thức

Đối với ma trận 2×2

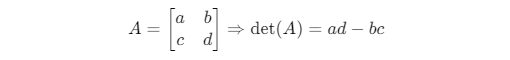
Đối với ma trận 3×3

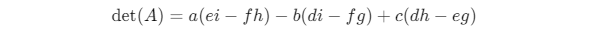
(hoặc dùng phương pháp Sarrus để dễ nhớ hơn)

Đối với ma trận lớn hơn (n×n)

Có 2 cách:

• Khai triển Laplace (Laplace Expansion) – dựa theo dòng hoặc cột

• Biến đổi ma trận về dạng tam giác và nhân các phần tử trên đường chéo

 Trong thực tế, sinh viên học STEM thường sử dụng phần mềm (Python/NumPy, MATLAB, máy tính Casio) để tính nhanh với ma trận lớn.

 

4. Ví dụ ứng dụng thực tế

Kiểm tra tính khả nghịch của ma trận

Cho:

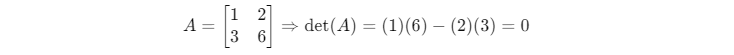
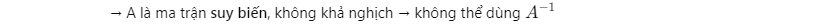
Giải hệ phương trình bằng phương pháp Cramer

Với hệ 2 phương trình 2 ẩn:

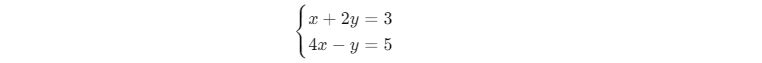
Gọi ma trận hệ số:

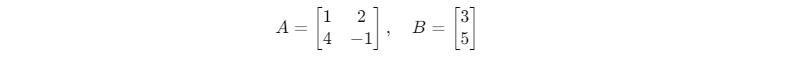
Tính định thức:

det⁡(A)=(1) (−1) − (2)(4)= −1− 8 = − 9 ≠ 0

→ Hệ có nghiệm duy nhất, tính được bằng công thức Cramer.

 

5. Những khó khăn học viên thường gặp

1. Chỉ học công thức, không hiểu bản chất
   → Không hiểu định thức phản ánh điều gì về không gian và ánh xạ

2. Tính toán thủ công dễ sai với ma trận lớn
   → Nhầm dấu, nhầm thứ tự khi khai triển Laplace

3. Không biết khi nào cần kiểm tra định thức
   → Dẫn đến sai lầm khi giải hệ phương trình hay kiểm tra khả nghịch

4. Lẫn lộn giữa định thức và phép nhân phần tử
   → Ví dụ: nghĩ rằng định thức là tích các phần tử chéo, điều này chỉ đúng trong một số trường hợp

 

6. Cách học hiệu quả 

✅ Bắt đầu từ trực quan hình học
→ Hình dung định thức là thể tích (hoặc diện tích) của hình không gian được tạo bởi các vector.
→ Hiểu ý nghĩa = dễ nhớ + áp dụng đúng

✅ Dùng phần mềm tính toán hiện đại
→ Học cách dùng Python (NumPy), MATLAB hoặc GeoGebra để thực hành
→ Tránh sai sót thủ công, tập trung vào tư duy

✅ Luyện các ví dụ gắn liền với ứng dụng thực tế
→ Thay vì làm toán trừu tượng, facingX giúp bạn làm các bài toán AI, vật lý, kinh tế có sử dụng định thức

✅ Học phân biệt giữa "cách tính" và "lý do phải tính"
→ Không chỉ biết cách bấm máy, mà hiểu “tại sao cần định thức ở đây?”

 

Kết luận – Khi định thức không chỉ là một con số

Trong lần đầu tiếp xúc, định thức có thể trông giống như “một phép toán kỹ thuật khô khan”. Nhưng khi bạn học đúng cách, bạn sẽ nhận ra: định thức không chỉ là một con số – nó là chỉ dấu về sự sống động hay suy biến của cả một không gian.

Bạn không học định thức để làm vài bài kiểm tra.
Bạn học định thức để:

• Biết một hệ phương trình có thể giải hay không

• Biết một ma trận có thể đảo ngược hay không

• Biết một không gian có chiều thật hay chỉ là ảo tưởng

• Và sau cùng, để hiểu bản chất thật sự của các phép biến đổi trong thế giới toán học – và cả thực tế.

Tại facingX, chúng tôi đồng hành cùng bạn để không chỉ vượt qua khó khăn của những con số,
mà còn mở ra cánh cửa tư duy khoa học vững chắc – thứ mà bất kỳ sinh viên nào cũng cần nếu muốn học tập và thành công ở môi trường quốc tế.

Chúng tôi không chỉ giúp bạn giỏi Toán. Chúng tôi giúp bạn hiểu thế giới thông qua Toán.

---