Từ vật lý lượng tử, cơ học kết cấu, thị trường tài chính, đến học sâu (deep learning), eigenvalues và eigenvectors là trái tim toán học của mọi biến đổi phức tạp.
Giá trị riêng và vector riêng – Khám phá những trục xoay ẩn sau mọi hệ thống
1. Mô tả tổng quan
Trong toán học, có những khái niệm không dễ tiếp cận nhưng lại ẩn chứa những hiểu biết cốt lõi để hiểu được thế giới vận hành thế nào.
Eigenvalues (giá trị riêng) và eigenvectors (vector riêng) là một ví dụ như vậy.
Chúng giúp chúng ta trả lời:
-
Vì sao một hệ động học dao động ổn định hoặc phân rã?
-
Làm sao để nén ảnh mà vẫn giữ lại thông tin quan trọng nhất?
-
Mô hình AI “học” bằng cách nào từ dữ liệu khổng lồ?
Từ vật lý lượng tử, cơ học kết cấu, thị trường tài chính, đến học sâu (deep learning), eigenvalues và eigenvectors là trái tim toán học của mọi biến đổi phức tạp.

2. Nội dung cốt lõi cần nắm
✅ Vector riêng là gì?
Một vector riêng của ma trận A là một vector không đổi hướng sau khi bị biến đổi bởi A. Thay vì xoay, nó chỉ kéo dài hoặc rút ngắn:
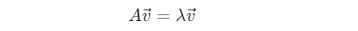

Đây là “trục xoay cố định” mà toàn bộ không gian bị xoay quanh nó.
✅ Giá trị riêng là gì?
Là hệ số λ thể hiện mức độ co giãn (stretching) hay phản hướng của vector riêng sau phép biến đổi:
-
Nếu λ>1: kéo dài
-
Nếu 0<λ<1: thu ngắn
-
Nếu λ<0: đảo ngược hướng
✅ Làm sao tìm được chúng?
-
Giải phương trình đặc trưng:
det(A−λI)=0
→ Tìm nghiệm λ của phương trình bậc n
-
Với mỗi λ, giải:

→ Tìm tập các vector riêng tương ứng
3. Trực quan và ý nghĩa hình học
-
Ma trận tuyến tính thường xoay – kéo – nén các vector.
-
Nhưng sẽ luôn tồn tại một vài vector không đổi hướng – đó chính là vector riêng.
Ví dụ: trong không gian 3D, khi bạn xoay một vật thể, có một trục xoay cố định – các điểm trên trục này chỉ “xoay tại chỗ”.
→ Trục đó chính là eigenvector, còn tốc độ xoay chính là eigenvalue.
4. Ứng dụng thực tế mạnh mẽ
Trong Machine Learning (PCA – Principal Component Analysis)
→ Dùng eigenvectors để xác định hướng chính của dữ liệu
→ Loại bỏ nhiễu, giảm chiều, giữ lại thông tin quan trọng nhất
Trong Cơ học và Vật lý
→ Dự đoán dao động riêng (natural frequencies) của công trình
→ Thiết kế tránh cộng hưởng trong cầu, nhà cao tầng, máy móc
Trong Tài chính – Phân tích danh mục đầu tư
→ Xác định “yếu tố ẩn” chi phối thị trường
→ Dùng eigenvalues để đo rủi ro hệ thống
5. Những khó khăn học viên thường gặp
-
Không hiểu ý nghĩa hình học của eigenvector
→ Cảm giác nó là một khái niệm "ảo" thay vì là vector thật -
Khó khăn trong giải phương trình đặc trưng
→ Đặc biệt khi ma trận lớn và chứa nghiệm phức -
Không phân biệt được đâu là vector riêng, đâu là không phải
→ Vì có thể có vô số vector riêng cùng thuộc một giá trị riêng -
Không thấy được ứng dụng thực tế
→ Học sinh mất động lực vì tưởng chỉ là bài toán lý thuyết
6. Cách học hiệu quả với facingX
Tư duy hình học trước – công thức sau
→ Chúng tôi giúp bạn trực quan hóa eigenvectors như các trục xoay, hình ảnh động – để bạn “thấy” thay vì “thuộc”.
Dạy công cụ thực hành hiện đại: Python, MATLAB
→ Tập trung vào phân tích kết quả, không sa lầy ở đại số tay
Ứng dụng vào bài toán ngành bạn học
→ facingX giúp bạn xử lý tập dữ liệu tài chính, tín hiệu âm thanh, ảnh kỹ thuật số – áp dụng PCA, phân tích phổ, hoặc diagonalization
Bài giảng song ngữ – kết nối chương trình học quốc tế
→ Nếu bạn học chương trình bằng tiếng Anh/Đức/Nhật, chúng tôi đảm bảo bạn hiểu đúng thuật ngữ chuyên ngành, không lệch khái niệm
Kết luận – Khi không gian lên tiếng, bạn cần eigenvectors để hiểu nó nói gì
Giống như trong một đám đông hỗn loạn, eigenvectors là những giọng nói chính yếu, còn eigenvalues là mức độ ảnh hưởng của mỗi giọng nói đó.
Biết cách tìm và lắng nghe chúng, bạn hiểu được bản chất của hệ thống – cho dù đó là một tập dữ liệu, một kết cấu cơ khí, hay một mô hình tài chính.
Tại facingX, chúng tôi không bắt bạn học thuộc lòng phương trình – chúng tôi giúp bạn hiểu vì sao phương trình đó lại đúng, và nó có thể giúp bạn làm gì.
Vì thế, khi bạn học eigenvalues cùng chúng tôi, bạn không chỉ học để thi, bạn học để phân tích, tối ưu, và làm chủ hệ thống phức tạp trong thời đại dữ liệu.facingX – Học để hiểu, hiểu để ứng dụng, ứng dụng để vươn xa.