Vectors (Vector) – Nền móng của Đại số tuyến tính

Vectors (Vector) – Nền móng của Đại số tuyến tính

1. Mô tả tổng quan

Vector không chỉ là một khái niệm trừu tượng trong Toán học – đó là cánh cửa đầu tiên dẫn vào thế giới Đại số tuyến tính. Nếu ví Đại số tuyến tính như một ngôn ngữ để mô tả không gian và chuyển động, thì vector chính là chữ cái, âm tiết trong ngôn ngữ ấy.

Từ xử lý hình ảnh số, trí tuệ nhân tạo, mô hình tài chính cho đến vật lý lượng tử – vector hiện diện ở mọi nơi, mọi ngành nghề đòi hỏi tư duy logic và phân tích số liệu.

2. Nội dung chính cần nắm

Vector là gì?

• Vector là một đối tượng có độ lớn (magnitude) và hướng (direction).

• Trong không gian 2D, bạn có thể hình dung vector như một mũi tên từ điểm này tới điểm kia.

• Ví dụ:

   

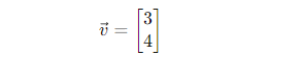
  biểu diễn một vector dài 5 đơn vị, nghiêng 53° so với trục hoành.

Các khái niệm then chốt:

• Phép cộng vector: Kết hợp hai vector để tạo ra một vector mới (nguyên tắc hình bình hành).

• Nhân vô hướng (dot product): Tạo ra một số thực, cho biết mức độ “đồng hướng” giữa hai vector.

• Tích có hướng (cross product): Tạo ra một vector mới vuông góc với hai vector ban đầu (chỉ dùng trong không gian 3 chiều).

• Độ dài (norm) và khoảng cách: Xác định độ lớn của vector, ứng dụng trong tính khoảng cách Euclid.

3. Những khó khăn thường gặp

1. Thiếu trực quan: Nhiều học sinh quen với số và phương trình, khi chuyển sang làm việc với các đối tượng hình học trừu tượng như vector sẽ dễ bị “mất phương hướng”.

2. Dễ nhầm giữa khái niệm đại số và hình học:

   • Ví dụ: Hiểu nhầm phép nhân vector là nhân từng phần tử (thay vì dot product).

   • Nhầm giữa hướng của vector với độ lớn.

3. Làm bài tập máy móc: Nhiều bạn học thuộc công thức nhưng không hiểu bản chất của dot product là đo độ "song song" giữa hai vector, hay norm là "chiều dài".

4. Cách học hiệu quả

- Hình ảnh hóa khái niệm
Dùng các công cụ trực quan như Geogebra, Desmos, hoặc vẽ tay để thấy vector "di chuyển" thế nào trong không gian. Học bằng hình ảnh sẽ giúp bạn nhớ lâu hơn so với học chay bằng ký hiệu.

- Liên hệ thực tế
Liên tưởng vector như các tình huống đời thường:

• Gió thổi về hướng Bắc – là một vector (có hướng, có độ mạnh).

• Di chuyển từ nhà đến trường – là một vector.

- Học thông qua ứng dụng
Đừng chỉ làm bài tập lý thuyết. Hãy thử áp dụng vector trong các bài toán:

• Tính khoảng cách giữa hai điểm

• Xác định góc giữa hai hướng đi

• Tìm hình chiếu vuông góc của lực (trong vật lý)

- Giải thích cho người khác
Nếu bạn có thể giải thích khái niệm vector cho một người chưa biết – nghĩa là bạn đã hiểu thật sự. Đây là kỹ thuật học cực kỳ hiệu quả được khuyến khích tại các đại học phương Tây.

5. Định hướng học Đại số tuyến tính hiệu quả 

Tại facingX.com, chúng tôi không chỉ giúp bạn hiểu khái niệm vector một cách trực quan và sâu sắc, mà còn:

• Kết nối bạn với giảng viên có kinh nghiệm giảng dạy Đại số tuyến tính tại các trường đại học châu Âu, Nhật, Úc.

• Cung cấp lộ trình học phù hợp với chương trình du học tại Đức, Canada, Úc (theo tiêu chuẩn các trường như TU Berlin, University of Toronto, Monash…).

• Hướng dẫn bạn học vector không chỉ để vượt qua kỳ thi, mà để sử dụng thực tế trong ngành AI, Kinh tế, và Kỹ thuật.